Have you ever found yourself in need of measuring various properties of triangles, but were unsure of how to go about it accurately? Understanding triangles can be essential for numerous real-world applications, whether it’s in construction, design, or even everyday tasks. A triangle calculator can quickly and efficiently help you find all necessary triangle measurements with just a few inputs.
 Triangle Calculator
Triangle Calculator
Triangle Calculator for Accurate Triangle Measurements
What Is a Triangle Calculator?
A triangle calculator is an online tool designed to compute various properties of a triangle based on initial measurements you provide. By inputting known side lengths and angles, it can calculate missing side lengths, angles, area, perimeter, semiperimeter, heights, medians, inradius, and circumradius. This can save enormous amounts of time and reduce the potential for manual calculation errors.
Directions for Use
Using a triangle calculator is intuitive. Here’s a simple guide to get you going:
- Input Values: Start by entering any three values into the input fields. At least one of these values must be a side length to ensure a unique solution.
- Select Units: Choose whether to perform the calculations in degrees or radians for the angles.
- Calculate: Press the “Calculate” button to see the results, including all missing values and a visual representation of the triangle.
- Show Calculation Steps: For an in-depth understanding, expand the “Show Calculation Steps” field to view the solution algorithm and formulas used.
This image is property of www.calculator.io.
Limitations on the Input Values
To ensure meaningful and accurate results, the input values must satisfy certain limitations:
- At Least One Side Length: Ensure one of the values is a side length to avoid infinite solutions.
- Angle Sum: The sum of entered angles must be less than 180° or π radians.
- Side Length Sum: For three side lengths, the sum of any two sides must exceed the length of the remaining side.
Calculation Example
Imagine you need to know if a portable ramp fits your truck’s height. You have sides measuring 1m and 0.8m with an angle of 85 degrees.
Given:
- Side b = 1m
- Side c = 0.8m
- Angle B = 85°
By entering these into the triangle calculator, you can determine if side A (the height) fits within the truck’s adjustable range (0.5m to 1m). The calculated missing side length turns out to be approximately 0.674m, which fits perfectly within the height range.

This image is property of www.calculator.io.
Triangle: Definition and Important Formulas
In geometry, a triangle is a plane figure formed by connecting three straight, non-parallel lines. It’s classified as a polygon with three vertices and three edges.
Conditions of Existence
A triangle exists if two key conditions are met:
- Triangle Inequality: The sum of the lengths of any two sides must be greater than or equal to the length of the third side.
- Angle Sum: The sum of the three internal angles must be exactly 180° or π radians.
Triangle Measurements
Understanding the fundamental measurements of a triangle is crucial. Here are the primary properties and corresponding formulas the triangle calculator uses:
Perimeter
The perimeter (p) is the sum of the lengths of all sides: [ p = a + b + c ]
Semiperimeter
The semiperimeter (s) is half of the perimeter: [ s = \frac ]
Area
The area (A) can be found using different methods. One common formula, given two sides and the included angle, is: [ A = \frac a \times b \times \sin(C) ]
Heights
Each triangle has three heights (altitudes) perpendicular to their respective opposite sides. Height ( h_a ), for instance, is: [ h_a = \frac ]
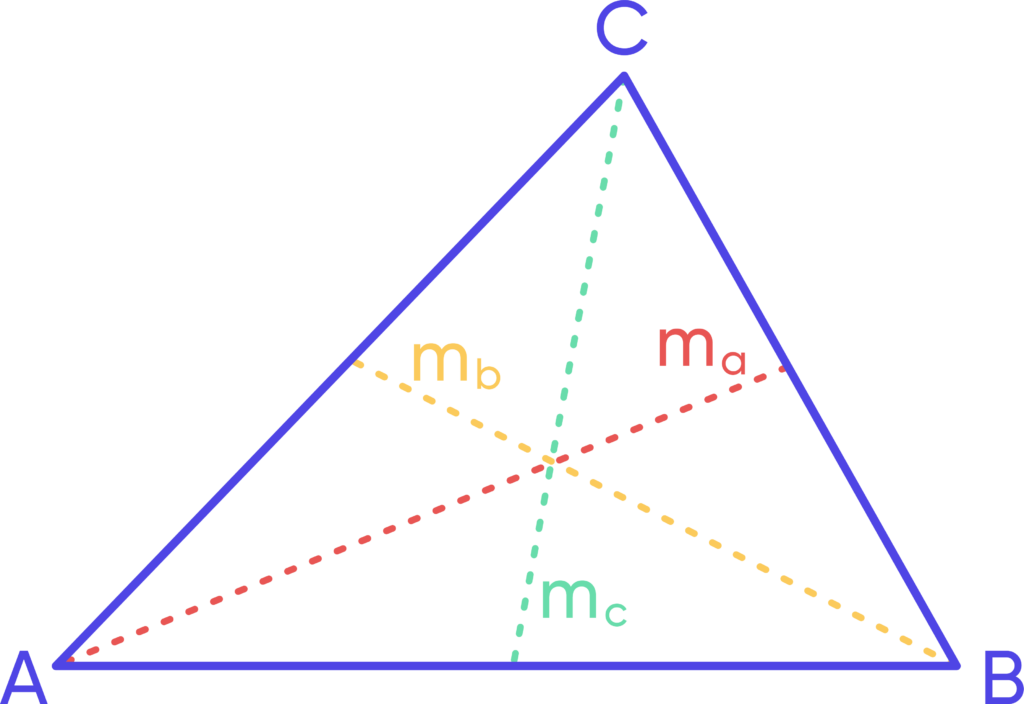
Medians
A median connects a vertex to the midpoint of the opposite side. For example, median to side a (( m_a )) is calculated as: [ m_a = \frac \sqrt ]
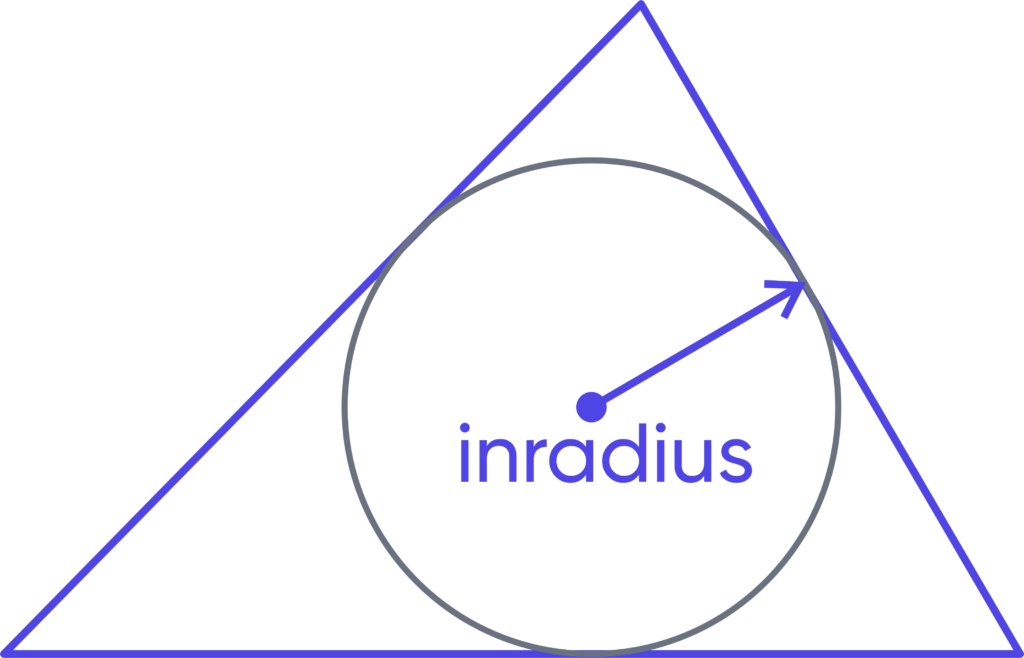
Inradius
The inradius (r) is the radius of the inscribed circle that touches all sides of the triangle: [ r = \frac ]
Circumradius
The circumradius (R) is the radius of the circumscribed circle passing through all the triangle’s vertices. The sine rule helps in finding it: [ 2R = \frac{\sin(A)} = \frac{\sin(B)} = \frac{\sin(C)} ]
This image is property of www.calculator.io.
Useful Trigonometric Rules
Sine Rule
This rule helps in relating the sides of the triangle to its angles: [ \frac{\sin(A)} = \frac{\sin(B)} = \frac{\sin(C)} ]
Cosine Rule
Useful for determining lengths and angles when dealing with non-right triangles: [ a^2 = b^2 + c^2 – 2bc \times \cos(A) ]
Summary
A triangle calculator is immensely useful for quick, accurate, and detailed computations related to triangles. By simply entering any three significant values—ensuring at least one value is a side length—you can unlock a full suite of triangle properties, aiding tasks varying from academic studies to practical projects.
Understanding triangles and their properties, using the calculator method simplifies these often intricate calculations ensuring you get precise results fast. The formulas included here guide you to make manual calculations if you prefer, but for effortless and error-free results, using the calculator is highly recommended.
Feel confident to handle any triangle measurement needs that come your way by leveraging the triangle calculator. With just a few inputs, you can unlock a world of geometric insights that might otherwise take much longer to uncover! Enjoy making accurate and efficient triangle measurements with this powerful tool.
