What’s the easiest way to calculate the distance between two points on a plane? Whether you’re a student trying to finish a math assignment or someone interested in the fascinating world of geometry, knowing how to find the distance between two points is both useful and rewarding. Let’s explore the distance formula, how to use a calculator for quick results, and real-world applications that bring this concept to life.
 Distance Formula Calculator
Distance Formula Calculator
Understanding the Distance Formula Calculator
Mathematics can sometimes feel like a jigsaw puzzle where the pieces fit together once you know the rules and formulas. The distance formula is a fundamental component that helps measure the space between two points on a plane. By utilizing the distance formula calculator, you can quickly and accurately find the distance without manually crunching numbers. This tool simplifies the calculation process by utilizing the tried-and-tested Euclidean distance formula.
This image is property of www.calculator.io.
How Does the Distance Formula Calculator Work?
The calculator is like your magical math companion. It computes the shortest path between two distinct points using their coordinates. Designed to work in two dimensions, the calculator requires you to input the x and y coordinates of both points. Let’s break this down further to see the magic formula it uses:
The Euclidean Distance Formula
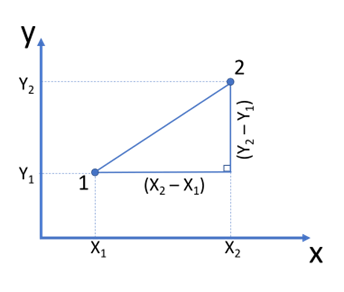
The secret sauce behind finding the distance lies in the revered Euclidean distance formula. This formula has been a staple in geometry for measuring straight-line distances between two locations on a plane:
[ d = \sqrt{(X₂ – X₁)^2 + (Y₂ – Y₁)^2} ]
In this equation, (d) represents the distance between the two points, ((X₁, Y₁)) are the coordinates of the first point, and ((X₂, Y₂)) are the coordinates of the second point. This formula works by summing up the squared differences of each coordinate and taking the square root of their total.
Directions for Using the Calculator
Using a distance formula calculator is incredibly straightforward, especially if you want to make the most out of your time. Here’s a step-by-step guide to seamlessly determine the distance between any two points:
- Enter Coordinates: Begin by inputting the x and y coordinates of the points. The first point’s coordinates go into the fields labeled (X₁, Y₁), and the second point’s into (X₂, Y₂).
- Format Guidelines: Enter each point’s coordinates separated by a comma. For instance, if a point has an x-coordinate of 4 and a y-coordinate of 5, enter it as “4,5”. Utilize decimal points to separate whole numbers from decimals when necessary, e.g., “4.5,7”.
- Precision in Inputs: Ensure only integers or decimals are used. Avoid fractions as they are not supported.
- Calculate: Press the “Calculate” button. The calculator will provide the distance instantly along with a detailed breakdown of the solution.
Unpacking the Euclidean Distance Formula
The origins of the distance formula come from Euclidean geometry, where distances and angles form the foundation of understanding spatial relationships.
Derivation of the Formula
The Euclidean distance formula finds its roots in the Pythagorean theorem. When analyzing the two points on a Cartesian plane, a right triangle emerges by drawing perpendicular lines from the points to the axes. The distance forms the hypotenuse of this triangle, while the legs represent the differences in x and y coordinates:
- Horizontal Distance: (X₂ – X₁)
- Vertical Distance: (Y₂ – Y₁)
By applying the Pythagorean theorem:
[ d^2 = (X₂ – X₁)^2 + (Y₂ – Y₁)^2 ]
Solving for (d) provides the formula we use today.
Examples of Calculation
Understanding through examples often cements concepts better than just theoretical knowledge. Let’s walk through some examples to see how this formula comes to life.
Example 1: Basic Coordinates
Consider two points: Point 1 at (3, 1) and Point 2 at (5, 7). Using the Euclidean distance formula, you can find the distance as follows:
[ d = \sqrt{(5 – 3)^2 + (7 – 1)^2} = \sqrt = \sqrt = \sqrt \approx 6.32 ]
Notice how the calculation remains the same even if you switch the order of the points, proving the formula’s flexibility.
Example 2: Involving Negative Coordinates
Now let’s tackle a case with negative coordinates. Find the distance between Point 1 (-4, 2) and Point 2 (6, -6). The calculation follows:
[ d = \sqrt{(6 – (-4))^2 + (-6 – 2)^2} = \sqrt = \sqrt = \sqrt \approx 12.8 ]
This example showcases the formula’s robustness even with negative values.
This image is property of www.calculator.io.
Real-life Applications
It’s intriguing to see mathematical formulas leap from paper to real-life applications. The Euclidean distance formula transcends abstract theories and becomes immensely useful for practical situations.
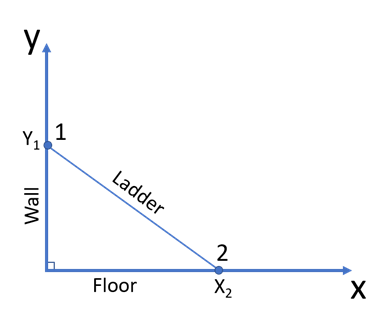
Example in Architecture: A Ladder Scenario
Imagine a ladder leaning against a wall, forming a triangle with the floor and the wall. Suppose the ladder reaches the wall at Point (0, 2) and touches the floor at (3, 0). To find the ladder’s exact length:
[ d = \sqrt{(3 – 0)^2 + (0 – 2)^2} = \sqrt = \sqrt = \sqrt \approx 3.6 ]
Here, the ladder’s length depicts the real-world application of the theoretical formula.
Extending the Distance Formula to 3D Space
Are you curious about measuring distances in three-dimensional spaces? The beauty of the Euclidean formula is its adaptability beyond two dimensions. In a 3D world, with points designated by coordinates (X₁, Y₁, Z₁) and (X₂, Y₂, Z₂), the distance expands into:
[ d = \sqrt{(X₂ – X₁)^2 + (Y₂ – Y₁)^2 + (Z₂ – Z₁)^2} ]
This expansion caters to more complex calculations involving depth, a rather exciting twist that makes this formula a mathematician’s delight in real-world calculations.
Related Tools and Calculators
In the realm of mathematics, the distance formula calculator stands as merely one tool amongst many. Acquainting yourself with other calculators could elevate your computational prowess:
- Speed Calculator: Determine the speed with its fundamental relationship to distance and time.
- Kinetic Energy Calculator: Explore physics with this tool designed to calculate movement energy.
- Pace Calculator: Perfect for health enthusiasts keen on monitoring their athletic performance.
- Velocity Calculator: Combine speed and direction for a comprehensive understanding.
Each of these tools, accessible online, provides intuitive interfaces for seamless calculation experiences.
Conclusion
Understanding and applying the distance formula doesn’t just boost your mathematical confidence; it prepares you for diverse real-world scenarios. From classroom assignments to architectural projects, mastering this calculator fuels your potential in both academic and professional fields. By harnessing a user-friendly calculator, you’re not just simplifying a process—you’re tapping into a richer understanding of geometry and its boundless possibilities. Now, the next time you’re curious about measuring a distance, you’ll know exactly which formula to use and how effortlessly you can achieve accurate results!