Do you ever find yourself puzzling over right triangles and wish there was an easier way to handle those tricky calculations? Understanding the Pythagorean Theorem and its applications can be quite a challenge if you’re tackling these geometric puzzles alone. Enter the Pythagorean Theorem Calculator Widget, a handy tool to simplify your calculations and make working with right triangles more approachable. Let’s embark on an informative exploration of this widget, shedding light on what it does and how you can use it to ease your mathematical tasks.
 Pythagorean Theorem Calculator
Pythagorean Theorem Calculator
What is the Pythagorean Theorem?
The Pythagorean Theorem is one of the cornerstones of geometry, especially when dealing with right triangles. This theorem, attributed to the ancient Greek mathematician Pythagoras, establishes a mathematical relationship between the three sides of a right triangle. Formally, it is expressed by the equation: (a^2 + b^2 = c^2). In this equation, (a) and (b) represent the lengths of the two shorter sides, or legs, of the triangle, while (c), the hypotenuse, is the longest side opposite the right angle.
This relationship is the key to solving various problems related to right triangles. The simplicity and elegance of the theorem have made it a vital tool not only in mathematics but also in fields like physics, engineering, and even art.
Making Use of the Pythagorean Theorem Calculator
Directions for Use
Using a Pythagorean theorem calculator can significantly enhance your understanding and application of this theorem. When you input the known side lengths into the calculator and press “Calculate,” it will return vital information including:
- The length of the unknown side.
- The non-90° angles in degrees and radians.
- The area of the triangle.
- The perimeter of the triangle.
- The length of the altitude perpendicular to the hypotenuse.
This tool presents a detailed solution with an option to expand for further explanation by showing calculation steps, making it easier to trace how each result is derived.
Entering Values and Conditions
The calculator accommodates both numerical and square root inputs, which is beneficial when solving problems requiring roots, such as when sides have values like ( \sqrt ) or ( 2\sqrt ). Remember, in right triangles, the lengths of the legs (a) and (b) must be less than the hypotenuse (c) for the theorem to correctly apply.
This image is property of www.calculator.io.
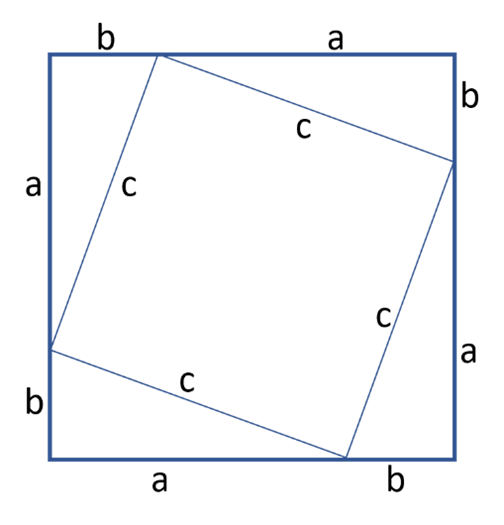
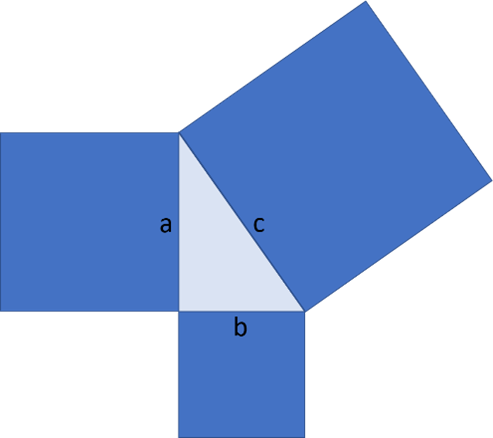
Proof of the Pythagorean Theorem
One of the engaging aspects of the Pythagorean theorem is its proof, which reveals the beauty of mathematical logic. Let’s prove the theorem using a geometric approach:
Imagine a square with side length ( (a + b) ). This square contains:
- A smaller square with side ( c ).
- Four right triangles with sides ( a ), ( b ), and ( c ).
The area of the large square can be calculated in two ways:
- By calculating the area using its side length: ((a + b)^2).
- By adding the area of the smaller square and the four triangles: (c^2 + 4 \times ( \frac )).
By equating these, and simplifying, you derive: (a^2 + b^2 = c^2), thus proving the theorem.
Practical Calculations Using the Theorem
Finding Sides, Angles, and More
Having two known sides of a right triangle makes finding the third side straightforward with the theorem:
- To find ( c ): ( c = \sqrt )
- To find ( a ): ( a = \sqrt )
- To find ( b ): ( b = \sqrt )
The non-right angles can also be found if all side lengths are known, using trigonometric functions:
- Angle opposite ( a ) (( \angle \alpha )): (\angle \alpha = \arcsin(\frac)) or (\angle \alpha = \arccos(\frac))
- Angle opposite ( b ) (( \angle \beta )): (\angle \beta = \arcsin(\frac)) or (\angle \beta = \arccos(\frac))
These calculations give insight into the geometric structure of the triangle beyond just side lengths, helping in applications involving angles.
Calculating Area and Perimeter
The area of a right triangle is straightforwardly half the product of its two legs: ( A = \frac ). Meanwhile, the perimeter sums up all sides: ( P = a + b + c ).
Determining the Altitude to the Hypotenuse
If all sides are known, calculating altitude to the hypotenuse uses this formula: ( h = \frac ). The altitude provides another viewpoint of the triangle’s structure, often helpful in advanced geometric calculations.
This image is property of www.calculator.io.
Real-Life Applications
The real power of the Pythagorean theorem shines in practical, everyday scenarios. It’s a necessity in construction, architecture, and various fields of engineering. For instance, if you need to fit an object through a diagonal space, you can use the theorem to determine if it will fit.
Example: Moving Objects
Suppose you need to check if a 4.5-meter ladder fits in a truck that measures 4 meters by 3 meters. Using the theorem:
- Calculate the diagonal (hypotenuse) of the truck’s interior: ( c = \sqrt = 5 ) meters.
Here, a 4.5-meter ladder fits since the truck’s diagonal extends to 5 meters.
Additional Insight and Calculations
To illustrate further possibilities, consider a right triangle where ( a = 4 ), ( b = 3 ), and ( c = 5 ). For this triangle:
- Area: ( A = \frac = 6 )
- Perimeter: ( P = 3 + 4 + 5 = 12 )
- Altitude to hypotenuse: ( h = \frac = 2.4 )
- Angle opposites:
- (\angle \alpha = \arcsin(\frac) = 53.13^\circ)
- (\angle \beta = \arcsin(\frac) = 36.87^\circ)
These calculations enhance your understanding of right triangles and illustrate how the Pythagorean theorem is vital for precise geometric analysis.
Conclusion
Finding solutions with the Pythagorean theorem doesn’t have to involve tiresome manual calculations. The Pythagorean Theorem Calculator Widget is a perfect assistant, handling calculations swiftly and providing comprehensive results. This tool not only simplifies complex problems, making them more accessible but also facilitates deeper understanding. Whether you’re an architecture enthusiast, a student, or someone dealing with geometric problems occasionally, embracing this widget can save time and improve accuracy in mathematical endeavors.