Have you ever wondered how you can easily find the slope of a line, whether for a mathematical problem or a real-world application like construction or landscaping? The solution is right at your fingertips with the Slope Calculator. This comprehensive online tool is designed to simplify your mathematical calculations and provide you with accurate results in no time. Let’s explore how this tool works, its various features, and how you can make it a part of your mathematical toolkit.
 Slope Calculator
Slope Calculator
This image is property of www.calculator.io.
Slope Calculator Overview
The Slope Calculator is a user-friendly online tool that helps you find the slope of a straight line by using the slope formula. Additionally, it can calculate other essential characteristics such as point coordinates, incline angle, and line length, provided you know the slope and at least one point.
Understanding the Slope
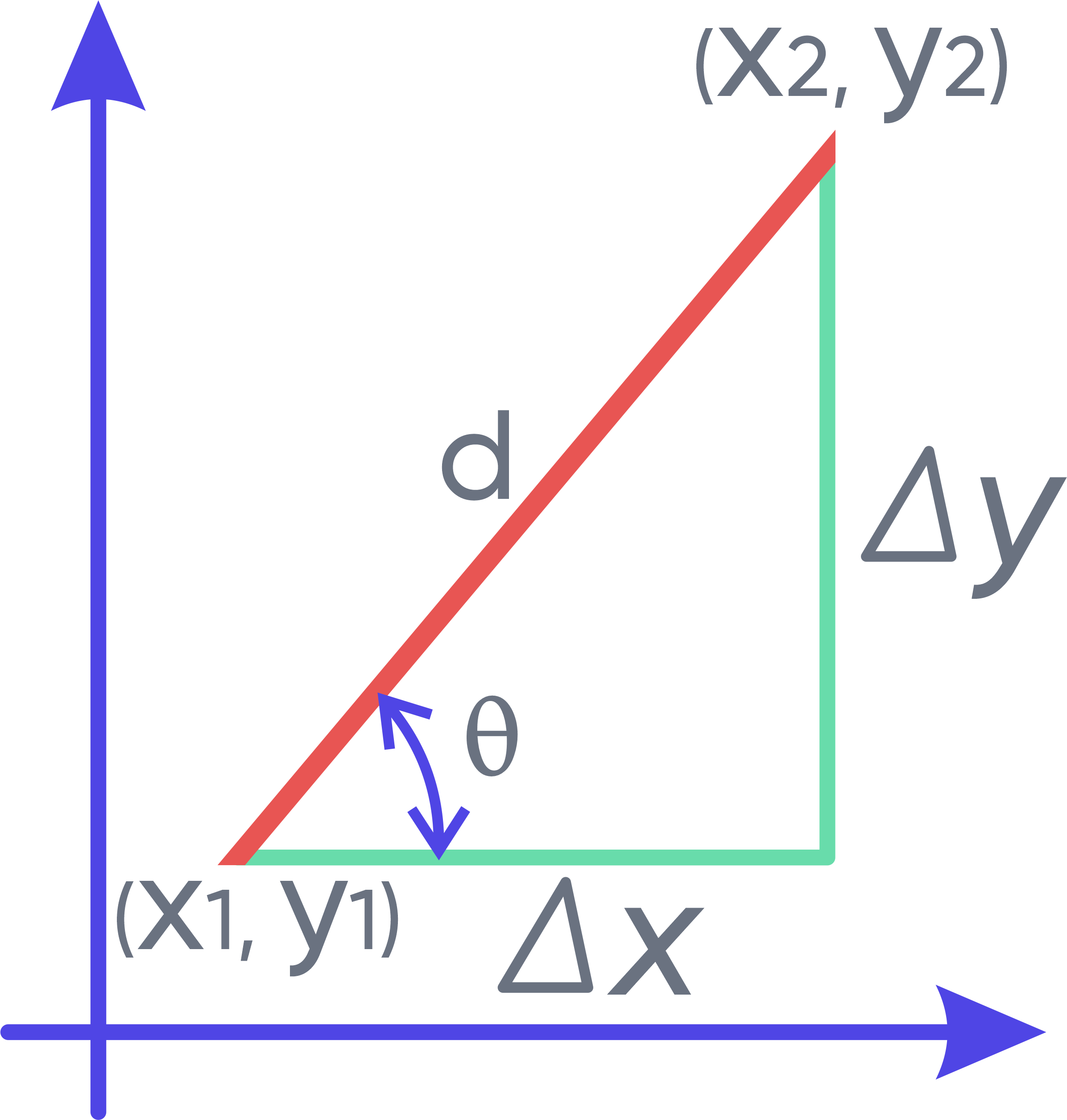
In mathematics, the slope of a line is defined as the change in the vertical coordinate (y-coordinate) relative to the change in the horizontal coordinate (x-coordinate). This value, denoted by ( m ), tells you how steep a line is and in which direction it runs.
Uses of the Slope Calculator
The Slope Calculator can be incredibly useful in various scenarios, such as:
- Geometry and algebra assignments
- Engineering designs
- Architectural plans
- Landscape projects
- Everyday tasks requiring angle and slope calculations
Notations Used
To use this tool effectively, let’s break down the key notations you’ll encounter:
| Symbol | Meaning |
|---|---|
| ( m ) | Slope of the line |
| ( x_1, y_1 ) | Coordinates of the first point on the line |
| ( x_2, y_2 ) | Coordinates of the second point on the line |
| ( \Delta x ) | Change in the horizontal coordinate: ( x_2 – x_1 ) |
| ( \Delta y ) | Change in the vertical coordinate: ( y_2 – y_1 ) |
| ( \theta ) | Angle of incline of the line in degrees |
| ( d ) | Length of the line |
Directions for Use
Using the Slope Calculator is straightforward. You can choose between two calculation methods:
- When the coordinates of two points on the line are known.
- When the coordinates of one point and the slope or inclination angle are known.
If Two Points are Known
- Input the known coordinates of the points into the respective fields.
- Click “Calculate.”
- The calculator will then provide:
- The slope ( m )
- The inclination angle ( \theta )
- The length of the line ( d )
- The changes in coordinates ( \Delta x ) and ( \Delta y )
- The equation of the line will also be displayed, along with a graphical representation.
If One Point and the Slope are Known
- Input the known coordinates of the point, the distance, and the slope or angle of incline ( \theta ).
- If both ( m ) and ( \theta ) are inputted, the calculator will prioritize ( m ).
- Click “Calculate.”
- The calculator will provide:
- The coordinates of the second point ( x_2, y_2 )
- The changes in coordinates ( \Delta x ) and ( \Delta y )
- The length of the line ( d )
- If slope ( m ) was used, the calculator provides ( \theta ) and vice versa.
- The equation of the line with a visual plot.
Calculating the Slope
Slope Formula
The slope formula is essential to find the slope of any given line. Given two points ((x_1, y_1)) and ((x_2, y_2)), the formula is: [ m = \frac = \frac{\Delta y}{\Delta x} = \tan(\theta) ]
Line Equation
A linear equation can be expressed in the following forms:
- Slope-Intercept Form: [ y = mx + b ] Here, ( b ) represents the y-intercept of the line.
- Point-Slope Form: [ y – y_1 = m(x – x_1) ] This is useful for finding the y-intercept when you know the slope ( m ) and one point on the line.
Characteristics of Slope
- If the line rises from left to right (( y_2 > y_1 ), ( x_2 > x_1 )), ( m ) is positive: line is increasing.
- If the line falls from left to right (( y_2
